![]() Ольга Постник
Ольга Постник
Формирование математических представлений средствами игровых технологий (кубики Никитина, Блоки Дьенеша, палочки Кюизенера)
▼ Скачать + Заказать документы
Формирование математических представлений средствами игровых технологий (кубики Никитина, Блоки Дьенеша, палочки Кюизенера.)
Уважаемые коллеги, я предлагаю, чтобы наша сегодняшняя встреча прошла под девизом: «Не лишайте ребенка радости играть, помните, что вы сами были детьми».
Публикация «Формирование математических представлений средствами игровых технологий (кубики Никитина, Блоки Дьенеша, палочки Кюизенера)» размещена в разделах
- Блоки Дьенеша
- Кубики. Игры с кубиками
- Математика. Математические представления, ФЭМП
- Никитин Б. П. Развивающие игры Никитина
- Палочки Кюизенера
- Темочки
- Конкурс для воспитателей и педагогов «Лучший мастер-класс» июнь 2017
Ребёнок по своей природе исследователь, экспериментатор. Его «Почему? Как? Где?» порой ставят в тупик неискушённых взрослых. Существует множество способов предоставить детям возможность самостоятельно открыть причину происходящего, докопаться до истины, понять принцип, логику решения поставленной задачи и действовать в соответствии с предложенной ситуацией.
Удовлетворять естественные потребности ребят в познании и изучении окружающего мира, их неуемную любознательность помогут игры-исследования.
Педагоги разных стран адаптируют и развивают технологии использования давно известных российских и зарубежных дидактических средств (развивающие игры Никитина, логические блоки Дьенеша, счётные палочки Кюизенера и др., расширяя горизонты мирового образовательного пространства.
Палочки Кюизенера – это счетные палочки, которые еще называют «числа в цвете», цветными палочками, цветными числами, цветными линеечками.
Комплект состоит из 10 пластмассовых призм различных цветов и размеров.
В семейство «красных» входят числа 2, 4, 8, т. е. кратные двум.
В семейство «синих» входят числа 3, 6, 9,т. е. кратные трем;
В семейство «желтых» входят числа 5,10, т. е. кратные пяти;
Наименьшая палочка в наборе имеет длину 1 см и является кубиком.
Кубик белого цвета — целое число, укладывается по длине любой палочки.
Цветные палочки являются многофункциональным пособием, которое позволяет «через руки» ребенка формировать математические понятия. Палочки Кюизенера позволяют решать следующие задачи:
• Познакомить с понятием цвета (различать цвета, классифицировать по цвету).
• Познакомить с понятием величины, длины, высоты, (упражнять в сравнении предметов).
• Познакомить с последовательностью чисел натурального ряда.
• Освоение прямого и обратного счета.
• Познакомить с составом числа (из единиц и двух меньших).
• Усвоить отношения между числами (больше - меньше на.)
• Познакомить со свойствами геометрических фигур.
• Развивать пространственные представления (слева, справа, выше, ниже и т. д.).
• Развивать логическое мышление, память, внимание, мелкую моторику.
Использовать метод Кюизенера довольно просто. В этом и прелесть. А еще одно преимущество состоит в том, что использовать игровые материалы можно уже с детьми от 1 года и проводить занятия на развитие внимания, памяти, мышления, речи, логики. Палочки выступают для ребенка просто игрушками.
Важно, что действия с палочками производятся ребенком сначала бесцельно, а затем приобретают смысл и конечную цель. Из них можно построить любую конструкцию, сложить их в виде пирамиды или разместить как столбики.
Занятия нужно проводить ежедневно. Для детей раннего возраста коробку для материалов лучше сделать в виде контейнера с отдельными секциями для палочек одинакового цвета и размера.
По окончанию работы малышам самим придется расселить всех «жителей» по их домикам, а этот процесс, в свою очередь, поможет сформировать у детей чувство ответственности и необходимость порядка.
Начинается любая игра со знакомства. Для начала предложите малышам посмотреть, что за посылку им прислал сказочный герой. Пусть сами распечатают коробку с игрой. Обратите их внимание на то, что палочки живут каждая в своем домике и им этот домик очень нравится. Они очень веселые и любят встречаться все вместе, чтобы поиграть, но потом непременно возвращаются к себе в домик.
На начальном этапе палочки используются как игровой материал. Игры и упражнения состоят в группировке палочек по разным признакам (цвету, размеру, сооружении из них построек, различных изображений на плоскости. В результате дети осваивают состав комплекта, цвета соотношения.
Задания
- Найдите палочку того же цвета, что и у меня. Какого они цвета?
- Выложите чередующиеся палочки : красная, желтая, красная, желтая (в дальнейшем ритм усложняется).
- Выложите несколько палочек, предложите ребенку их запомнить, а потом, пока ребенок не видит, спрячьте одну из палочек. Ребенку нужно догадаться, какая палочка исчезла.
Можно выкладывать из палочек на плоскости дорожки, заборы, поезда, квадраты, прямоугольники, предметы мебели, разные домики, гаражи.
Задания
- Выложите высокий (низкий забор, лесенку.
- Выложите любое изображение.
На данном этапе используется альбом «Волшебные дорожки», в котором предлагаются увлекательные задания с палочками.
Дети очень любят сказки, и на 3 году жизни они знают хорошо несколько. Среди сказок выбираем хорошо знакомую малышу и проигрываем ситуацию с героями. Например, «Колобок».
Сначала можно выложить дорожку для Колобка из палочек желтого цвета (румяный и поджаристый Колобок, затем построить схематически домики для зверей, с которыми встретился Колобок. У Зайца будет домик меньше, чем у Волка, а у Медведя – самый большой. Сравнить эти домики и обратить внимание малыша на то, что больший домик мы строили из палочек большей длины и т. д.
Когда ребенок освоит комплект палочек, они выступают как пособие для маленьких математиков. И тут дети учатся постигать законы загадочного мира чисел и других математических понятий.
Задания
- Найдите в наборе самую длинную и самую короткую палочку.
- Выложите несколько палочек. «Какая самая длинная? Какая самая короткая?»
- Найди любую палочку, которая короче синей, длиннее красной
- Постройте поезд из вагонов разной длины, начиная от самого короткого и заканчивая самым длинным. Какого цвета вагон стоит пятым, восьмым. Какой вагон справа от синего, слева от желтого. Какой вагон тут самый короткий, самый длинный? Какие вагоны длиннее желтого, короче синего.
- Выложите голубую и розовую палочки. На сколько голубая палочка длиннее розовой?
Такие задания с палочками позволяют освоить понятия величины, длины, предметов.
Рассмотрим возможности палочек при освоении детьми пространственных отношений.
- Выкладывайте палочки, следуя инструкциям: положите красную палочку на стол, справа положи синюю, снизу желтую и т. д.
- Выложите башню, используя по одной палочке каждого цвета. Какая палочка лежит выше (ниже) других? Какая лежит над черной, голубой (под бордовой) Какая по цвету палочка, если она лежит между голубой и оранжевой?
- Положите синюю палочку между красной и желтой, а оранжевую слева от красной, розовую слева от красной.
Палочки Кюизенера позволяют знакомить детей со свойствами геометрических фигур.
Задания
- Выложите из красных палочек квадрат и прямоугольник. Чем отличаются фигуры?
- Рассмотрите образец и по памяти выложите из палочек фигуру.
- Выложите четыре белые палочки, чтобы получился квадрат. На основе этого квадрата можно познакомить ребенка с долями и дробями. Покажи одну часть из четырех, две части из четырех. Что больше - или 2/4?
Следующим этапом в работе с палочками Кюизенера является развитие количественных представлений и освоение счета.
Задания
• Выложите лесенку из 10 палочек от меньшей (белой) к большей (оранжевой) и наоборот. Пройдитесь пальчиками по ступенькам лесенки, можно посчитать вслух от 1до 10 и обратно.
• Выложите разное количество голубых и красных палочек. Каких больше (меньше? Использовать разные способы сравнения.
• Найдите палочку соответствующую числу (1 - белая, 2 - розовая и т. д.). И наоборот.
• Выложите синюю палочку. Сколько белых палочек уложится в синей палочке?
Игры с палочками Кюизенера
Игра «Мы строители». Смотрим по уровню развития ребенка. Начинать можно с простых фигур. Построить, например, домик. Попросить ребенка построить:
Такой же дом
Больший (меньший) дом
Синий дом (розовый, зеленый)
Игра «Закончи рисунок». Обучение малыша вообразить конечный результат и закончить картинку. Взрослый выкладывает половину рисунка, разделив картинку осью посередине. Задача ребенка – дополнить рисунок такими же элементами и закончить картинку. Это могут быть различные предметы, например, тарелка, мяч, кувшинчик и т. д.
Игра «Кто самый внимательный». На развитие внимания, памяти. Выложить перед ребенком несколько палочек (до 3-4 для начала, представить, что это конфеты. Пусть посмотрит на них и запомнит. Затем попросите его отвернуться, уберите одну палочку, ребенок повернется и должен сказать, какую «конфетку» вы съели.
Игра «Составь узор». На занятии развивается творческое воображение, слуховое восприятие, пространственное мышление, речь. Вы вместе составляете узор. По очереди называете палочку, которую нужно взять и указываете ее место в узоре. Следующим ходом ребенок тоже дает вам подобные задания.
Игра «Найди и покажи». Развитие логического мышления. Здесь как угодно разнообразно можете придумывать задания. Тоже лучше чередовать задания с ребенком. Например, найди палочку короче синей, но длиннее красной. Или покажи палочки, которые можно разместить между розовой и желтой.
Игра «Выложи предмет по образцу». Это занятие предполагает полную свободу действий и полет фантазии. Сначала можно действовать по просьбе взрослого: сложи слона, девочку с корзинкой, троллейбус с красными окошками и т. д. А потом можно составлять, что хотите.
Таким образом, использование палочек Кюизенера позволяют ребёнку овладеть способами действий, необходимых для возникновения у детей элементарных математических представлений.
Хочу познакомить вас с ещё одним уникальным материалом, который даёт возможность формировать в комплексе все важные для умственного развития, и в частности математического мыслительные умения на протяжении всего дошкольного обучения - это логические блоки Дьенеша, разработанные венгерским психологом и математиком Дьенешем для подготовки мышления детей к усвоению математики.
Дидактический набор состоит из 48 объемных геометрических фигур.
Самое главное в этих блоках – это различие по четырем свойствам: формой, цветом, размером и толщиной.
Почему я взяла для работы именно эти блоки? Потому что в процессе разнообразных действий с логическими блоками дети овладевают различными мыслительными умениями, важными как в плане предматематической подготовки, так и с точки зрения общего интеллектуального развития.
Игры с логическими блоками позволяют решать следующие задачи:
– познакомить с формой, цветом, размером, толщиной объектов.
– развивать пространственные представления.
– развивать логическое мышление, представление о множестве, операции над множествами (сравнение, разбиение, классификация, абстрагирование, кодирование и декодирование информации).
– развивать умения выявлять свойства в объектах, называть их, обобщать объекты по их свойствам, объяснять сходства и различия объектов, обосновывать свои рассуждения,
– развивать познавательные процессы, мыслительные операции,
– воспитывать самостоятельность, инициативу, настойчивость в достижении цели,
– развивать творческие способности, воображение, фантазию, способности к моделированию и конструированию.
– развивать речь.
– успешно овладеть основами математики и информатики.
Все игры и игровые упражнения можно разделить на 4 группы с постепенным усложнением:
– для развития умений выявлять и абстрагировать свойства;
– для развития умений сравнивать предметы по их свойствам;
– для развития действий классификации и обобщения;
– для развития способности к логическим действиям и операциям.
Работу с блоками Дьенеша следует начинать с младшей группы. Для начала детям предлагаются самые простые игры, цель которых освоение свойств, освоение таких выражений, как «Такой же», «Не такой».
Давайте представим, что вы дети 2-3 лет.
1. Покажите блок такого же цвета как этот.
2. Найди блок такой же формы.
3. «Угости игрушку». Разложи фигуры таким образом, чтобы у каждой игрушки были фигуры только одного цвета, одного размера и т. п. 4. Берём круг. Расположите все фигуры красные внутри круга, а все синие – снаружи. 5. Выложите блоки с определенной последовательностью : синий, красный, синий, красный. Или круг, треугольник, круг, треугольник.
А теперь представим, что вы дети 3-4 лет.
1. Разложи фигуры по их свойствам, собери все красные, или все круглые.
2. Усложняем задание: Найди такой же блок по цвету и форме.
3. Найди не такой блок по цвету; по форме; по цвету и форме. Данный вид игры проводим индивидуально.
4. Более сложный вариант: Найди такую же, как этот по цвету и форме, но другого размера. Проводим индивидуально.
5. Можно использовать задания с игрушкам. Предлагаем детям разделить, чтобы у Мишки все фигуры были красные, у зайца – желтые и т. д. В конце игры дети должны ответить на вопрос: «Какие фигурки у Мишки?», «Какие фигуры у зайца?» и т. д.
6. В этом же возрасте начинается работа по схемам. Предлагаются самые легкие.
Вот мы с вами разобрали несколько игр для детей младших групп.
Теперь представим, что вы дети 4-5 лет.
В данном возрасте дети знакомятся с символами свойств.
1. Покажи такую же фигуру по цвету и форме; по цвету, форме и размеру.
Знакомятся с понятием «НЕ».
2. Покажи фигуру по моделям (используется модель с «НЕ»). Покажите – не круг и не квадрат, не синий и не толстый блок, не круглый и не красный и т. п.
3. Усложняется работа по схемам по стрелочкам. Постройте цепочку по схеме.
Игра «Построй дорожку». Цель: развивать умение выделять свойства в предметах, абстрагировать эти свойства от других, следовать определенным правилам при решении практических задач.
Ход игры: перед детьми – таблица, на полу – блоки.
Игровая задача : построить дорожки для пешеходов и автомобилей в городе. Правила построения дорожек записаны в таблице (демонстрация таблиц)
2 вариант «Дорожки»
Цель: развитие умений выделять и абстрагировать цвет, форму, размер, толщину, сравнивать предметы по заданным свойствам.
Ход игры: на полу по кругу расставлены три домика для Ниф-Нифа, Наф-Нафа, Нуф-Нуфа. Между ними нужно проложить дорожки так, чтобы поросятам удобно было ходить в гости друг к другу. Но дорожки нужно строить по правилам.
Например, первую дорожку построить так, чтобы не было в ней рядом фигур одинакового цвета. Вторую – чтобы не было фигур одинакового размера и формы. Третья дорожка состоит из блоков, чередующихся по толщине, и всех четырехугольников.
Для поддержания интереса детей взрослый меняет игровые задачи : построить мост через реку, сделать праздничную гирлянду, составить поезд из блоков – вагончиков и др. (В старшем дошкольном возрасте дети могут рисовать в тетрадях дорожки, цепочки, мостики из фигур).
4. Игра по карте: «Довези машину до гаража»
В этом возрасте ребенок манипулирует двумя свойствами: Например, Чебурашка не любит красные игрушки и не хочет играть с круглыми. Какую он возьмет?
5. Игра «Домик». Лист расчертите на 6 квадратов – это будут комнаты. В 5 комнат положите блоки определенных цветов, а шестую оставьте пустой, Ребенок должен догадаться, какого цвета фигура должна быть в этой комнате.
6. Игра «Что лишнее?» Разложите перед детьми 4-5 блоков. В ряду один лишний – он может отличаться цветом, формой. Ребёнок должен объяснить, почему он думает, что эта фигура лишняя.
7. Игра «Группы». Нарисуйте два пересекающихся круга. Все синие фигуры могут лежать в левом круге, а все треугольники в правом. В середину нужно положить фигуры, которые подходят и к первому и ко второму кругу. Проблема возникнет, когда ребенок возьмет синий треугольник, куда его положить? Отлично, если ребенок сам догадается, что фигура принадлежит обоим множествам. Это задание только кажется простым, но очень важно для формирования умения разделить множества предметов на разные группы.
Для детей старшей и подготовительной группы все задания усложняются. Самое главное, что в этом возрасте дети должны выполнять игровую задачу быстро и качественно. А также ребенок в этом возрасте уже умеет описать свойства любого блока с противоположной стороны. Например: Что можно рассказать о желтом прямоугольнике? (ответы присутствующих). Ответ: он не красный, не синий, некруглый, не треугольный, неквадратный, нетолстый, немаленький. Что можно сказать о красном треугольнике?
А сейчас я вам предлагаю, немного подвигаться. Проведем игру с блоками Дьенеша.
«Посадим красивую клумбу»
Материал : набор блоков Дьенеша, 4 обруча, карточки с обозначениями признаков фигур и отрицанием признаков.
Ход игры: В одном обруче размещаются 24 фигуры блоков Дьенеша – это рассада.
На другом краю зала размещаются три обруча так, чтобы они пересекали друг друга. В каждый обруч кладется карточка с обозначением признака: цвет, форма, величина, Дети берут по одному блоку и «сажают в ту «клумбу», карточка на которой соответствует признаку этого блока, если у блока совпадают два признака, то его помещают в пересечение 2 обручей, а если совпали все три признака, то в пересечение 3 обручей. Если же фигура не соответствует ни одному признаку, то её помещают вне обручей. За каждый правильно размещенный блок ребенок получает очко, выигрывает тот, кто наберет больше очков.
Затем дети решают различные игровые задачи, предложенные взрослым : засаживают цветами палисадник. Например, посадить цветы так, чтобы на красной клумбе росли все красные цветы, на синей - все круглые, на желтом - все большие цветы.
Игра «Помоги фигурам выбраться из леса»
Цель. Развитие логического мышления, умения рассуждать.
Материал. Логические фигуры, или блоки, таблицы.
Ход игры: Перед детьми таблица. На ней изображен лес, в котором заблудились фигурки. Нужно помочь им выбраться из чащи.
Сначала дети устанавливают, для чего на разветвлениях дорог расставлены знаки. Не перечеркнутые знаки разрешают идти по своей дорожке только таким фигурам, как они сами; перечеркнутые знаки — всем не таким, как они, фигурам. Затем дети разбирают фигуры (блоки) и по очереди выводят их из леса. При этом рассуждают вслух, на какую дорожку каждый раз надо свернуть.
Для поддержания интереса взрослый ставит перед детьми разнообразные игровые задачи, наделяет фигуры и блоки различными образами. Например, каждая фигура - Дюймовоч-ка (нужно помочь ей выбраться из мышиной норы) или блоки-корабли (надо вывести их из бушующего моря) и т. п.
Развивающая игра представляет собой многоплановое, сложное педагогическое явление: она является и игровым методом обучения детей, и формой обучения, и самостоятельной игровой деятельностью, и средством всестороннего воспитания личности ребенка. Борис Павлович и Елена Алексеевна Никитины педагоги – новаторы, жившие в Советском Союзе, разработали интересную систему развивающих игр.
Этот союз позволил разрешить в игре сразу несколько проблем, связанных с развитием творческих способностей:
- игры Никитина могут стимулировать развитие творческих способностей с самого раннего возраста;
- задания-ступеньки игр Никитина всегда создают условия, опережающие развитие способностей;
- ребенок развивается наиболее успешно, если он каждый раз самостоятельно пытается решить максимально сложные для него задачи;
- игры Никитина могут быть очень разнообразны по своему содержанию и, кроме того, как и любые игры, они не терпят принуждения и создают атмосферу свободного и радостного творчества;
Сегодня я хочу познакомить с развивающими играми Б. П. Никитина и поиграть в них вместе с вами.
К развивающим играм Никитина относятся игры : «Уникуб», «Кубики для всех»,«Сложи узор», «Сложи квадрат» и другие.
Игра «Кубики для всех»
Игра состоит из 7 фигурок, различных по форме : одна фигура из 3, а остальные из 4 кубиков каждая.
Игра учит мыслить пространственными образами (объемными фигурами, умению их комбинировать и является значительно более сложной, чем игры с обычными кубиками.
Практическая часть для педагогов
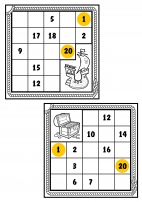
Перед вами рисунок-задание, постройте из фигурок точно такую же модель, как нарисовано.
Игра «Сложи узор»
Игра состоит из 16 одинаковых кубиков. Все 6 граней каждого кубика окрашены по-разному в 4 цвета. Это позволяет составлять из них 1-, 2-, 3- и даже 4-цветные узоры в громадном количестве вариантов. Эти узоры напоминают контуры различных предметов, картин, которым дети любят давать названия. В игре с кубиками дети выполняют 3 вида заданий.
Сначала учатся по узорам-заданиям складывать точно такой же узор из кубиков. Затем ставят обратную задачу: глядя на кубики, нарисовать узор, который они образуют. И, наконец, третье – придумывать новые узоры из 9 или 16 кубиков, каких еще нет в книге, т. е. выполнять уже творческую работу.
В этой игре хорошо развивается способность детей к анализу и синтезу, этим важным мыслительным операциям, используемым почти во всякой интеллектуальной деятельности, и способность к комбинированию, необходимая для конструкторской работы.
Практическая часть для педагогов
Перед вами рисунок-задание, сложите из кубиков такой же узор (лебедь, узор).
Игра «Сложи квадрат»
Игра напоминает «пазл» - из отдельных разрозненных частей, необходимо сложить нечто целое. Этим целым является квадрат.
Игра представлена тремя вариантами различной степени сложности. Они различаются количеством составных частей квадрата. Квадрат-образец присутствует только в первом варианте. Игровые задания составлены таким образом, что по ним можно работать со всеми вариантами игры. Они расположены в порядке усложнения.
Практическая часть для педагогов
1. Выложите на стол все квадраты (части) и перемешайте их.
2. Рассортируйте по цвету все кусочки квадрата и разложить на кучки (попросите ребенка назвать цвета и оттенки, сосчитать).
3. Теперь нужно правильно сложить квадраты (можно устроить соревнования на время.
Никитинские игры рассчитаны на совместную игру ребенка и взрослого. Степень их вариативности высока, их можно подстраивать под себя, под свой уровень и интересы. Каждая игра предоставляет возможность подумать над тем, как ее расширить, какие новые задания к ней добавить, как ее усовершенствовать. Такая вариативность заданий заранее предусмотрена, и переход к творческой работе над самими играми будет тем успешнее, чем выше уровень творческих способностей ребенка.
Что ж, выбор методов и материалов за вами. Пробуйте, экспериментируйте, ищите. Главное, чтобы вашим детям было интересно, и вы видели результат своих трудов.