Использование знаковой системы в математическом развитии старшего дошкольного возраста (1 фото)

Наталья Баринова
Использование знаковой системы в математическом развитии старшего дошкольного возраста
▼ Скачать + Заказать документы

Использование знаковой системы в математическом развитии детей старшего дошкольного возраста

Воспитатель делится опытом работы по обучению детей действиям замещения, способам обозначения предмета при помощи знаков, а также обучения детей выполнения задания по алгорит му.

Публикация «Использование знаковой системы в математическом развитии старшего дошкольного возраста» размещена в разделах

• Математика. Математические представления, ФЭМП
• Развитие ребенка. Материалы для педагогов
• Старшая группа
• Темочки

Ознакомление со знаковой системы в развитии ребёнка – начало большого пути, ведущего к использованию им математических символов, нотных знаков, компьютерных программ, которое он может применить во всех сферах своей деятельности

Исследования психологов, посвящённые усвоению математики дошкольниками, показывают, что затруднения, возникающие у детей, связаны с недостаточным пониманием смысла чисел и арифметических знаков

(+ -Поэтому мы уделили большое внимание ознакомлению детей со знаковой системой так как обучение детей математическим знаниям, а, следовательно, и развитие логического мышления, происходит на основе эталонов, знаков, символов и т. д.

Исходя из результатов педагогического мониторинга детей, проведенного в ходе наблюдения за ними на занятиях, в режимных моментах, в свободном общении со сверстниками, а также через собеседование, мы поставили перед собой задачи:

1. Обучение детей умению находить собственные способы и средства разрешения поставленной математической задачи.

2. Умение интерпретировать математические отношения и зависимости через знаковое обозначение.

3. Овладение детьми способность выполнять математические действия через использование алгоритма.

Свою работу по решению данных задач начали с ознакомления детей с геометрическими фигурами и их признаками, а также установления логических связей и зависимостей между ними. С этой целью мы широко использовали пособие блоки «Дьенеша».

В играх предлагали детям таблицы и карточки, которые означали основные признаки геометрических фигур (цвет, форму, величину, толщину). Карточки – коды и являлись знаковыми единицами.

В ходе работы поощряли детей за подробное словесное описание свойств геометрических фигур. Например: «Я положил круг красного цвета большой и толстый».

Чтобы научить детей давать полное словесное описание, выкладывали карточки – коды постоянно в определенной последовательности:

ФОРМА ЦВЕТ ВЕЛИЧИНА ТОЛЩИНА

Освоение детьми признаков фигур проводила через усложнение игр на классификацию (сначала по 2 свойствам, затем - по 4) и выделение закономерностей в создании группировок.

Результатом первого этапа работы по формированию развития логического мышления у наших детей стало умение классифицировать материал по разным признакам зрительно и при помощи осязания (игра «чудесный мешочек», умение комментировать свои действия.

В настоящее время знакомим детей с классификации геометрических фигур по четырем признакам.

Вводим элемент отрицания, т. к. дети седьмого года жизни должны уметь отражать в речи способ группировки, используя при этом слова : все, «кроме».

Для формирования у детей понятия об «отрицании» некоторых свойств с усвоение знаковой помощью частицы «не», ввели карточки – символы отрицания, т. е. карточки с перечеркнутым изображением признака (не толстый, не маленький, не красный и др.)

Для этого детям предлагался простейший вариант игры с обручами, при этом предлагались задания:

*в желтый обруч положить все фигуры кроме маленьких, т. е. большие

*в зеленый обруч положи фигуры не треугольные, не квадратные

не прямоугольные, т. е. - круги.

Для развития логического мышления детей использовали математическое пособие «Хитрые карточки», изготовленное по книге А. А. Смоленцевой «Математика до школы», состоящее из набора кодовых карточек, обозначающих разные свойства предметов

Только после этого упражнения детям предлагались задачи с признаками отрицания : «Кате подарили котенка: не черного и не белого, не с желтыми и не с синими глазами, с длинным хвостом. Какого котенка подарили Кате?» Для решения этой задачи требуется 16 карточек.

Решение задачи:

Кате подарили полосатого, с зелеными глазами и длинным хвостом котенка

В результате проделанной работы, дети научились: выделять свойства геометрических фигур; группировать их по основным признакам; давать словесные описания.

В содержании обучения детей математическим знаниям преобладают логические задачи, ведущие к познанию закономерностей простых алгоритмов.

Слово «алгоритм» означает предписание о порядке выполнения действий.

Самым простым видом алгоритма, который мы использовали для развития у детей логического мышления, является выполнение детьми математических действий при помощи указательного знака «стрелка».

Так в игре «Угадай-ка», зарисовывая фигуры, дети выделяли закономерность в изменении количества и расположения фигур при помощи указывающих стрелок.

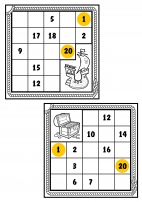
Далее детям было предложено задание «Математические бусы». Инструкция давалась в стихах:

Из разных цифр я сделал бусы,

А в тех кружка, где чисел нет

Поставь их, чтобы правильный

Получить ответ.

Стрелкой указывалась последовательность выполнения действий.

Затем задание усложнялось:

Из разных цифр я сделал бусы,

А в тех кружках, где чисел нет,

Расставьте минусы и плюсы,

Чтоб данный получить ответ.

В дальнейшем детям предлагались задания другой направленности.

Были предложены задания на развитие способности комбинирования. Смысл их заключался в поиске разных сочетаний при изменении местоположения предметов (предметы располагались до изменения в одном виде, а после изменения – в другом).

Например, в игре «Одна клетка» требовалось найти конечное расположение фигур после одного передвижения (в соседнюю клетку, т. е. детям предлагалось самостоятельно найти фигуру, которую требовалось самостоятельно переместить в соседнюю свободную клетку. Стрелка на карточке указывала, что передвижение можно делать только в соседнюю клетку.

После проведения серии игр многие дети научились выделять закономерности в расположении фигур, цифр и делать простейшие умозаключения о конечном результате выполнения задания по указанию стрелки.

С целью овладения детьми понятиями «больше», «меньше», «равно», умение давать точную словесную оценку мы использовали условные обозначения – знаки (- + =)

Для того, чтобы научить детей соотносить величины между собой, мы использовали математическую ситуацию «О чем говорят числа?»

Спрашивали детей:

«Вы слышали, как разговаривают числа? Давайте послушаем»

Встретились три числа: 5, 6 и 7. О чем они говорят?

Число 5 говорит числу 6 -«Я меньше тебя» 5 6

Число 6 говорит числу 7 - «Я меньше тебя» 6 7

Числа умеют разговаривать, но не словами, а значками.

Нарисуем этот разговор:

Число 5 говорит числу 7 - «Я меньше тебя» 5 7

Тоже нарисуем этот разговор 5 6 7

Вопрос к детям. Что скажут все три числа друг другу?

Дети приходят к выводу, что любое число относительно, т. е. одновременно может быть и больше и меньше (шесть больше пяти, но меньше семи).

После того, как детям были даны первоначальные образцы словесного объяснения решений, мы на занятии стали использовать новую математическую ситуацию «Как разговаривают числа?» Учили детей разным способам записи отношений «больше», «меньше» между числами. Спрашивали детей: «Как будут разговаривать числа, нарисованные на карточках?

Затем дети самостоятельно выбирали карточки с цифрами и рисовали их разговор с соседями. Предлагали детям разнообразные схемы, отражающие отношения между числами.

Обучая детей ориентироваться в пространстве с помощью планов, схем; обозначению пространственных отношений на листе бумаги, мы провели ряд занятий.

Особое внимание уделяли отношению мест, занимаемых предметами в пространстве по отношению к другим предметам (сзади, спереди, слева, справа).

Такие отношения мы изображали с помощью наглядной модели (план, схема, где сами предметы были обозначены при помощи тех или иных условных заместителей (геометрические фигуры, значки). Дети легко понимали, что такое план комнаты, план участка. Использование планов, схем развивало логическое мышление детей.

Постепенно дети овладевали внешними формами замещения, появилась возможность применять наглядные модели в уме, представлять при их помощи то, о чем рассказывают взрослые. А это и является показателем высокого умственного развития ребенка.

Предлагали детям, знакомые со старшей группы игры с использованием планов – схем : «Принеси карандаш», «Как пройти к замку?», «Найди игрушку» и т. д. На плане значком отмечалось место, где спрятан предмет, и детям нужно было узнать это место, но дополнительно вводилось усложнение. Это либо увеличивалось количество предметов на плане, либо план предлагался в перевернутом на 180 градусов виде, либо был обозначен стрелочками маршрут. Такие игры детям очень нравятся.

Таким образом, в результате проведенной работы по использованию знаковой системы в развитии логического мышления детей мы добились определенных результатов. Дети научились:

o Выполнять действия по знаковым обозначениям, определять последовательность действий в играх;

o Читать схему, способ и путь выполнения действий;

o Оперировать знаками +, -, = при вычислениях;

o Пользоваться алгоритмом.

Задачей на будущее является: более широкое использование в дальнейшем различных видов алгоритмов не только в математике, но и в других видах детской деятельности (природоведческой, речевой, изобразительной и т. д.)

Список литературы:

1. Венгер Л. А., Дьяченко О. Т., Говорова Р. И. Игры и упражнения по развитию умственных способностей у детей дошкольного возраста. – М. : Просвещение;

2. Данилова В. В., Рихтерман Т. Д., Михайлова З. А. Обучение математике в д/с. – М. : Академия, 1997;

3. Михайлова З. А., Смоленцева А. А. «Математика до школы», СПб, Детство- Пресс, 1998

4. Михайлова З. А. «Игровые задачи для дошкольников», СПб «Детство- Пресс», 1999

5. Тихомирова Л. Ф., Басов А. В. «Развитие логического мышления детей», Ярославль, 1995